La parallaxe
On parlera ici principalement de parallaxe annuelle.
La parallaxe annuelle est une méthode qui permet de connaître
la distance d'une étoile en mesurant un angle.
De la théorie ...
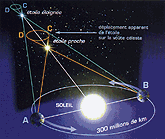 La distance d'un astre peut être donnée par sa parallaxe. Il s'agit de l'angle sous lequel est vue la distance Terre-Soleil depuis cet astre. Cet angle est obtenu en mesurant la direction de l'astre à six mois d'intervalle (voir schéma ci-contre). La distance d'un astre peut être donnée par sa parallaxe. Il s'agit de l'angle sous lequel est vue la distance Terre-Soleil depuis cet astre. Cet angle est obtenu en mesurant la direction de l'astre à six mois d'intervalle (voir schéma ci-contre).
Durant cette période, la Terre a parcouru la moitié de son orbite annuelle. Entre la première et la deuxième observation, elle se trouve de part et d'autre du Soleil et le même astre est ainsi vue sous 2 angles différents. Cet écart angulaire est, par construction, le double de la parallaxe. La connaissance de cette parallaxe, ajoutée à celle de la mesure de la distance Terre-Soleil, donne immédiatement (à l'aide d'une formule trigonométrique, voir "Applications") la distance entre l'astre et la Terre.
Cette méthode s'applique aux objets du système solaire et aux étoiles proches. Il faut cependant préciser que dans le cas des étoiles, la parallaxe est toujours inférieure à 1" (1° divisé par 3600), donc difficile à mesurer. Au-delà de 1000 années-lumière, les parallaxes ne sont plus mesurables, d'autres méthodes sont alors utilisées.
... à la pratique
Ni dans l'Antiquité, ni au Moyen Âge, ni au cours de la révolution scientifique, ni même aux heures glorieuses de l'astronomie post-newtonienne, on ne put détecter cette variation parallactique. Néanmoins, la chasse à la parallaxe était lancée.
 Pour trouver cette parallaxe, Galilée avait mis au point une remarquable méthode, fondée sur une hypothèse très largement admise à l'époque, quoique fausse : les étoiles doivent être toutes de même luminosité. Les variations d'éclat entre elles traduisent des éloignements différents de notre Terre. Galilée choisit alors des couples d'étoiles, dont les composantes étaient en apparence très proches, mais de luminosité extrêmement différente. En observant les positions de ces couples d'étoiles, on devrait constater que la plus brllante est bien plus affecée que sa jumelle par le phénomène de parallaxe. Pour trouver cette parallaxe, Galilée avait mis au point une remarquable méthode, fondée sur une hypothèse très largement admise à l'époque, quoique fausse : les étoiles doivent être toutes de même luminosité. Les variations d'éclat entre elles traduisent des éloignements différents de notre Terre. Galilée choisit alors des couples d'étoiles, dont les composantes étaient en apparence très proches, mais de luminosité extrêmement différente. En observant les positions de ces couples d'étoiles, on devrait constater que la plus brllante est bien plus affecée que sa jumelle par le phénomène de parallaxe.
Appliquant la méthode de Galilée, plusieurs astronomes ont cru avoir réussi en décelant des déplacements mais ils se trompaient. Ces savants avaient-ils erré au point d'annoncer des variations angulaires qui n'auraient pas existées ? La réponse est que leurs étoiles suivaient bien annuellement une ellipse, mais celle-ci ne pouvait correspondre à l'ellipse parallactique.
Les ellipses décalées, plus grandes que celles attendues de la parallaxe, étaient dues à un phénomène que personne n'avait prévu, l'aberration stellaire qui résulte de la vitesse finie de la lumière. En effet, la combinaison de cette vitesse avec celle de l'orbite décale l'image que nous avons de l'étoile.
 Sans doute fallait-il un savant, à la fois mathématicien et astronome, pour découvrir les écarts issus de la parallaxe au sein même des écarts, supérieurs, dus à l'aberration stellaire. Bessel releva le défi au début du XIXe siècle. Il examina systématiquement durant 18 mois l'étoile double 61 Cygni, dotée d'un important mouvement propre connu, et analysa précisément les données, rendant à l'aberration stellaire ce qui lui revenait, et obtenant ainsi une variation angulaire résiduelle qu'il put enfin attribuer à la parallaxe (1838). Sans doute fallait-il un savant, à la fois mathématicien et astronome, pour découvrir les écarts issus de la parallaxe au sein même des écarts, supérieurs, dus à l'aberration stellaire. Bessel releva le défi au début du XIXe siècle. Il examina systématiquement durant 18 mois l'étoile double 61 Cygni, dotée d'un important mouvement propre connu, et analysa précisément les données, rendant à l'aberration stellaire ce qui lui revenait, et obtenant ainsi une variation angulaire résiduelle qu'il put enfin attribuer à la parallaxe (1838).
Pour transformer ces angles, extrêmement petits, en distance, encore fallait-il déterminer le rayon de l'orbite terrestre, c'est-à-dire la distance moyenne séparant la Terre du Soleil. A cette époque, celle-ci n'était connue qu'avec une précision toute relative et chacun pensait que des améliorations étaient à venir. Il parut donc naturel d'inventer une nouvelle unité de distance, le parsec, distance à laquelle la parallaxe est égale à 1". C'est la distance à laquelle on verrait le demi-grand axe de l'orbite terrestre sous un angle de 1".
A la fin des années 1980, on ne connaissait encore avec précision que les parallaxes d'environ 8000 étoiles, obtenues à partir de mesures directes. Grâce au satellite d'astrométrie européen Hipparcos, on connaît maintenant avec une précision de 0.001" les parallaxes d'environ 100 000 étoiles.
Applications
- La distance D d'une étoile au Soleil, exprimée en parsecs, est donnée par la relation suivante :
D = 1/ |
- D : distance Soleil-étoile en parsecs
-  : parallaxe annuelle exprimée en secondes de degré (") : parallaxe annuelle exprimée en secondes de degré (")
En supposant que l'on mesure la parallaxe annuelle d'une étoile à 0.125", quelle est sa distance au Soleil ?
D = 1 / 0.125
D = 8
L'étoile se trouve à 8 parsecs du Soleil. Pour trouver la distance en années-lumière ou en kilomètres, il suffit de convertir (voir l'article sur "Les unités de mesure des distances").
 - La distance D d'une étoile au Soleil, exprimée en l'unité de distance que l'on veut, est donnée par la relation suivante : - La distance D d'une étoile au Soleil, exprimée en l'unité de distance que l'on veut, est donnée par la relation suivante :
D = r /  |
- D : distance Soleil-étoile en l'unité choisie
- r : distance Terre-Soleil en l'unité choisie (la même que pour D)
-  : parallaxe annuelle exprimée en radian : parallaxe annuelle exprimée en radian
En supposant que l'on mesure la parallaxe annuelle d'une étoile à 0.125", quelle est sa distance au Soleil ?
D'abord, il faut convertir la parallaxe annuelle en radian.
angle en radian =  ( angle en degré / 180 ) => Remarque : ici ( angle en degré / 180 ) => Remarque : ici  est le nombre pi environ égale à 3.14 est le nombre pi environ égale à 3.14
angle en degré = angle en seconde de degré / 3600
Donc  = =  [ ( 0.125 / 3600 ) / 180 ] [ ( 0.125 / 3600 ) / 180 ]
En admettant que l'on choisit l'année-lumière comme unité, il faut trouver combien vaut r en années-lumière (al).
r en al = r en km / nombre de kilomètres en 1 année-lumière
r = 150 000 000 km
1 al = 9 500 000 000 000 km
Donc r en al = 150 000 000 / 9 500 000 000 000
Donc
D = ( 150 000 000 / 9 500 000 000 000 ) /  [ ( 0.125 / 3600 ) / 180 ] = 26.05 al [ ( 0.125 / 3600 ) / 180 ] = 26.05 al
L'étoile se trouve à 26 années-lumière du Soleil.
Vous pouvez essayer de calculer la distance à laquelle se situe l'étoile la plus proche du Soleil. Sa parallaxe annuelle est de 0.76". Cliquez ici pour voir la réponse.
L'étoile la plus proche du Soleil est Proxima du Centaure.
Elle se trouve à environ 4.29 années-lumière soit 1.32 parsec.
Cacher la réponse
Page non trouvée dans comprendre_pages
Auteur : Didier Walliang
Date de création : 28/02/01
Source : "Le grand livre du ciel" (BORDAS) et "Astronomie Pratique" (HACHETTE)
|

